leetcode-Wiggle Subsequence-376

For example, [1,7,4,9,2,5] is a wiggle sequence because the differences (6,-3,5,-7,3) are alternately positive and negative. In contrast,[1,4,7,2,5] and [1,7,4,5,5] are not wiggle sequences, the first because its first two differences are positive and the second because its last difference is zero.

Given a sequence of integers, return the length of the longest subsequence that is a wiggle sequence. A subsequence is obtained by deleting some number of elements (eventually, also zero) from the original sequence, leaving the remaining elements in their original order.

Examples:

Input: [1,7,4,9,2,5]
Output: 6
The entire sequence is a wiggle sequence.

Input: [1,17,5,10,13,15,10,5,16,8]
Output: 7
There are several subsequences that achieve this length. One is [1,17,10,13,10,16,8].

Input: [1,2,3,4,5,6,7,8,9]
Output: 2

Follow up:
Can you do it in O(n) time?

该题贪心和DP都能做

贪心策略1：3个点为一个局部条件，

不满足的去掉中间那么点，只关心3个数的斜率是否满足条件，用3个数来记录下标，记录逻辑上3个评定的数字

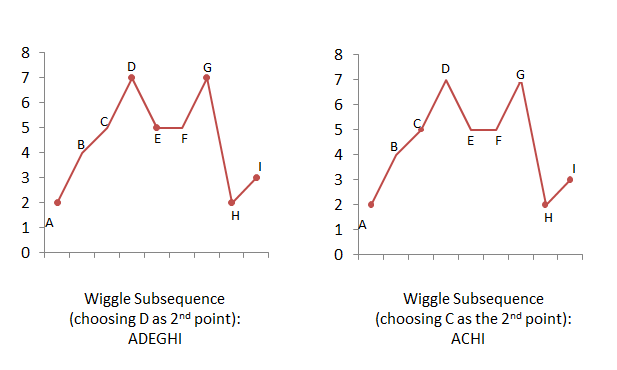
ABC时 贪心策略去掉B,反证：如果去掉A 那么A之前的上限提高了，更不会得到更优解，C同理，因此去掉B是最优

同理ACD时去掉C，……

if (nums.size() == 0)return 0;
		if (nums.size() == 1)return 1;
		if (nums.size() == 2)
		{
			if (nums[0] == nums[1])return 1;
			return 2;
		}


		int ret = 1;
		if (nums[0] != nums[1] && nums[1] != nums[2] && nums[2] != nums[0])ret++;
		int d = nums[2] - nums[1];

		int a = 2;
		int b = 1;
		int c = 0;
		int d2 = 0;
		for (int i = 2; i < nums.size(); i++)
		{
			a = i;

			d2 = nums[b] - nums[c];
			int d1 = nums[a] - nums[b];

			if (d1*d2 < 0)
			{
				ret++;
				d = a - b;
			}
			if (d2 != 0 && d1 != 0)
			{
				c = b;//V或者倒V的情况
				b = a;
			}
			else
			{
				if (d1 == 0 && d2 != 0){  b=a; }

				if (d2 == 0 && d1 != 0){ ret++; b = a;  }
				
	

			}
		}
		return ret;

还有更快的方法：仔细分析策略1,3个点中，a,b可以合为一个点，点c可以记录上一次有效数字的index

if (nums.size() < 2) return nums.size();

		int p = 0, len = 1;

		for (int i = 0; i < nums.size() - 1; ++i)
		{
			if (nums[i] == nums[i + 1]) continue;

			if ((nums[i] - nums[p])*(nums[i + 1] - nums[i]) <= 0) p = i, ++len;
		}

		return len;